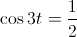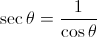In this section, we have learned about all sorts of processes used to solve trigonometric equations. Possibly the most difficult part of this process is when there are multiple angles in a trigonometric function. These require lots of deep thought and plenty of intuitive thinking.










These solutions, along with the other two previous ones are the solutions to this "fun" and "easy" trigonometric equation!
For example:

In order to solve this equation, we must wait until the VERY END to take care of the 3t. Therefore, we must solve the equation and isolate the variable.

Once we reach this point in the step-by-step process, we know that, on the unit circle,


Normally we would be finished with this equation and wold normally be content with these answers but the 3t is yet to be completed. Now that we have radian measures we can divide each by 3 to find our real solutions.After calculations, we come up with these answers:


Well would you look at that! We're done! .... Not so fast my friends.
Alongside the two solutions that we uncovered there are a few more hiding within the interval,
In order to find these other solutions we must add the periods using the coefficient within the trigonometric functions.
Period for this trigonometric function is as follows:
From here you should add this period to each of the solutions from earlier and you add to them the resulting solutions which here happen to be:




These solutions, along with the other two previous ones are the solutions to this "fun" and "easy" trigonometric equation!