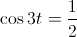5.4 Sum and Difference Formulas

Sum and Difference Formulas are best used when an angle isn't obvious on the unit circle.

The two main purposes of these formulas are finding exact values of other trig functions and simplifying expressions to find other identities

Sum and Difference Formulas for sin, cos, and tan:

Example 1:

Find the exact value of cos 75°

cos75°=cos(30°+45°)

=cos 30° cos 45° - sin 30° sin 45°

You can check your answer by plugging it into your calculator. cos 75° is about 0.259, so our answer is correct!

Example 2: Find the exact value of

Double-Angle Identities

Sine:



Cosine:

There are three different versions of the cosine double angle identity, which can be found by deriving from each other.

Original Identity:



To derive a new identity substitute:



New versions of identity:





Tangent:

Solving Trigonometric Equations Involving Multiple Angles

In this section, we have learned about all sorts of processes used to solve trigonometric equations. Possibly the most difficult part of this process is when there are multiple angles in a trigonometric function. These require lots of deep thought and plenty of intuitive thinking.

For example:

In order to solve this equation, we must wait until the VERY END to take care of the 3t. Therefore, we must solve the equation and isolate the variable.

Divide by 2.

Once we reach this point in the step-by-step process, we know that, on the unit circle,

Normally we would be finished with this equation and wold normally be content with these answers but the 3t is yet to be completed. Now that we have radian measures we can divide each by 3 to find our real solutions.After calculations, we come up with these answers:

Well would you look at that! We're done! .... Not so fast my friends.

Alongside the two solutions that we uncovered there are a few more hiding within the interval,

In order to find these other solutions we must add the periods using the coefficient within the trigonometric functions.

Period for this trigonometric function is as follows:

From here you should add this period to each of the solutions from earlier and you add to them the resulting solutions which here happen to be:

These solutions, along with the other two previous ones are the solutions to this "fun" and "easy" trigonometric equation!